Bayesian analysis

Bayesian analysis is a method of determining the relative likelihood of two or more alternative possibilities, based on Bayes' theorem of probability. In genetic counseling, it can be applied when determining the risk in a family where the genotype of some of the relevant relatives of the proband is unknown (it cannot be easily diagnosed), and therefore we cannot clearly establish carrier status in them.

Usage[edit | edit source]

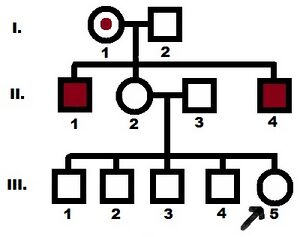
From the data obtained from the subject (III-5, marked with an arrow), it is not clear whether II-2 is a carrier or not. However, this data is essential for determining the risk that the subject is a carrier.

The use of Bayesian analysis in genetic counseling can be illustrated by the example of a family with hemophilia A , whose family tree is shown. To determine the probability of transmission in III-5, the relevant information is whether II-2 is a carrier or not. This figure cannot be determined from the information found, but intuition suggests that if III-5 has four healthy brothers, the probability that their mother is a carrier probably reduces this. Bayesian analysis helps us take data of a similar nature into account, because it takes into account certain important phenotypic information.

Calculation procedure[edit | edit source]

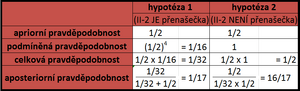
We calculate separately the II-2 probability for both hypotheses (variants), i.e. "II-2 is a carrier" and "II-2 is not a carrier", in a clear table with two columns. For both hypotheses, we will further determine the values of the following probabilities:

Bayesian analysis applied to the calculation of the probability of transmission in a relevant relative of an unknown genotype.

A priori probability is the initial probability of any hypothesis that it is correct without knowing anything more about the pedigree of a given family than what it seems to imply.

What is the probability that II-2 is/is not a carrier? II-2 is a carrier daughter, therefore P(non-carrier) = ½, P(carrier) = ½.

The conditional probability is in each column, under the hypothesis for that column, that the events that you know have already happened (ie, the facts that you have discovered about the family tree) could have happened given that the hypothesis at the beginning of the column is correct.

What is the probability that II-2 has four healthy sons for both hypotheses? The probability that a carrier will have a healthy son is ½, four healthy sons (½) 4. The probability that a "non-carrier" will have a healthy son is 1, four healthy sons 4 × 1.

The total probability is the product of the prior and conditional probability.

We calculate it by multiplying the a priori and conditional probability, see the relevant cell in the table.

Posterior probability pits both total probabilities against each other.

It is the ratio of the total probability of the hypothesis to the sum of both total probabilities of our hypotheses. It also follows that only the posterior probability values add up to 1.

Now we can easily calculate the risk for the proband:

risk of transmission in II-2: 1/17
transmission risk in the female proband (III-5) : ½ × 1/17 = 1/34

Summary[edit | edit source]

Using phenotypic information from the family tree, we were able to establish a specific value for the probability that the subject's mother is a carrier of hemophilia A, thus quantifying what seemed intuitively likely from the perspective of the family tree. The given example serves as an illustration, more detailed and complex cases are dealt with, for example, in the source literature.

Links[edit | edit source]

References[edit | edit source]

NUSSBAUM, Robert – MCINNES, Roderick – WILLARD, Huntington. Klinická genetika. 1. edition. Triton, 2004. ISBN 978-80-7254-475-2.