First law of Thermodynamics

Definition

For a given system is the 1st law of thermodynamics defined as:

$\Delta U=Q+W$

where $\Delta U$ is the total increment of the internal energy of a given system, $Q$ is the total heat received by the system from the surroundings and $W$ is the total work done by the surroundings on the system.

We often encounter formula in differential form.:

$\mathrm {d} U=\mathrm {d} Q+\mathrm {d} W$

The equation in differential form is not values changed over the duration of the whole process but over an infinitely short period of time.

Physcial perspective

This is the law of conservation of energy:

The energy by which the internal energy of the system increases cannot be generated out of nothing. The energy must be supplied to the system from outside (i.e., by its surroundings) in the form of heat Q or mechanical work W. In another words, during the exchange between the system and the surrounding, the energy does not arise or crease.:

$\Delta U-Q-W=0$

Use of the First Thermodynamical Law

The first law of thermodynamics is of great use in describing processes in an [[[ideal gas]]] in which can take palce various processes used in a practical part. In order to make their description and importance as clear as possible, we will introduce general parameters of the system on which the individual processes will be described:

System

1. is closed (it can not exchange the elements with its surrounding)
2. is not isolated (it can exchange the energy with its surrounding)
3. consists 1 mole
4. of the idealn gas.

Thanks to the first two conditions we can consider the formulation of the 1st law of thermodynamics mentioned above, thanks to the third condition we can neglect the term $n$ - l amount of substance (because $n=1$) - and thanks to the last condition, we do not have to consider losses caused by internal friction.

We talk about processes during which this system does not change one of its [[[state quantities]]], i.e. $\mathrm {d} =0$, where $A$ stands for a given quantity.

Isochoric process

Ischor

An action in which there is no change in volume is called isochoric, $\mathrm {d} V=0$, (from greek: isos - same and choros - space).

The formula is $\mathrm {d} W=p\mathrm {d} V=0$. From the first law of thermodynamics, after substitution, is the formula $\mathrm {d} Q=\mathrm {d} U$

and therefore all the supplied heat is consumed to increase internal energy $\Delta U$.

Dependency curve $p=p(V)$ for the isochoric process is called isochor.

Isothermal process

Ideal gas isotherms

A process in which there is no change in temperature is called isothermal $\mathrm {d} T=0$. (from greek: isos - same a therme - temperature/heat).

The formula is $\mathrm {d} U=C_{V}\mathrm {d} T=0$, where $C_{V}$ stands for molar heat capacity of the gas at a constant volume.

The formula for the first law of thermodynamics after substitution is $\mathrm {d} Q=-\mathrm {d} W$

and that is why all the supplied heat is consumed to do the work.

Dependecy curve $p=p(V)$ for the isothermical process is called isotherm.

Isobaric process

Isobar

A process in which there is no change in pressure is called isobaric (from greek "isos" - same a "baros" - pressure). The formula is $\mathrm {d} p=0$.

The equation of state gives us a mathematical description of the isobaric process in an ideal gas $V/T=konst.$, which is the so-called Gay-Lussac's Law.

The formula for calculation of the work done by gas is $\mathrm {d} W=p\mathrm {d} V$. After substituting the equation of the first law of thermodynamics, we get its form for the isobaric process. $\mathrm {d} Q=\mathrm {d} U+p\mathrm {d} V$

Dependancy curve $p=p(V)$ for the isobaric process is called isobar. Given the constant pressure value, the work done by the gas can be subtracted from the graph as area under the curve bounded by the initial and final values of the gas volume. This area is a graphical representation of the equation $\mathrm {d} W=p\mathrm {d} V$.

The heat received by an ideal gas in an isobaric process is equal to the sum of the increment of its internal energy and its work. From the point of view of the validity of the first law of thermodynamics, this process is the most complicated. None of the quantities involved in the first law of thermodynamics will be equal to zero (in the isochoric process, the work done by the ideal gas is zero, in the isothermal process, there is zero change in the internal energy of the gas during the given process). Practical use of the isobaric process as well as other thermodynamic processes can be found, for example, in diesel engines (Diesel's cycle).

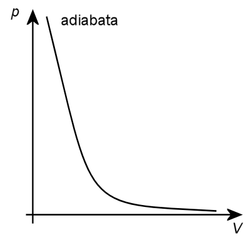
Adiabatic process

Adiabate

The formula for the adibatic process is $\mathrm {d} Q=0$. There is no heat exchange between the gas and the surrounding (as in isolated systems), or the action happens so quickly that no heat exchange can take place. Therefore, the plot is very complicated to be realized. Real processes tend to be on the border between isothermal and adiabatic processes (Polythropic process). Entropy does not change in adiabatic process.

After substituting the equation of the first law of thermodynamics:

$\mathrm {d} W=-\mathrm {d} U$

it can be seen that the system does its work at the expense of internal energy.

This equation could be further modified to get $pV^{\kappa }=$ constant.

Whereas $\kappa$ is Poisson's constant and can be expressed from the equation $\kappa =c_{p}/c_{V}$.

Such an equation establishes a dependence between variables $p$ and $V$ and thus allows the adiabatic process to be expressed also on the diagram (p, V). 

This curve is called adiabate. It is similar to an isotherm, but has a steeper course, which we derive from the isothermal equation $pV^{1}=$ constant while Poisson's constant $\kappa$ is bigger than one.

With adiabatic compression of gas in a vessel, work is done by the action of an external force on the piston. The temperature of the gas and its internal energy increase. During adiabatic expansion, gas does work and the temperature of the gas and its internal energy decreases. Adiabatic expansion is used to achieve low temperatures. Adiabatic compression is used in diesel engines. Adiabatic compression raises the temperature of the air to the ignition temperature of diesel, which ignites itself when injected into this air.

References

Related articles

• Thermodynamic laws

Source

• MARŠÁK, Zlatěk. Termodynamika a statistická fyzika. 3. vyd. Praha: Vydavatelství ČVUT, 1995, s. 23-25. ISBN 80-01-01401-0.

• Multimediální encyklopedie fyziky (MEF), 2006-2013, Jaroslav Reichl, Martin Všetička http://fyzika.jreichl.com/