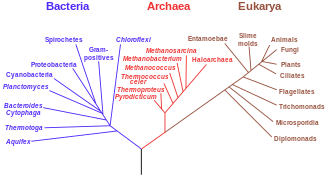
Phylogenetic tree construction

Phylogenetic tree

Phylogenetic tree is a graphic representation of relationships between different taxonomic units that can be assumed to have a common ancestor. Kinship relationships here are assessed on the basis of morphological or genetic similarity. Instead of taxonomic units, individual biological species or even individual genes can act directly in some trees.

The term tree is taken from graph theory, where it denotes a non-oriented continuous acyclical graph. We refer to branching points that are connected with two or more other branches as internodes. The remaining tips, which are associated with only one node, are called leaves or terminal taxa.

In the case of phylogenetic trees, each tip represents a particular taxonomic unit, and the branch between two nodes indicates the relationship between the taxonomic units that are represented by these leaves. Depending on the type of phylogenetic tree, the branch length may indicate the time of development or the degree of similarity between the respective taxonomic units.

Phylogenetic tree types

Unrooted phylogenetic tree

This type of tree depicts the relationships between taxonomic units without specifying their common ancestor.

Rooted phylogenetic tree

A rooted phylogenetic tree is a tree where one of the inner nodes has been identified as a root. This gave the branches of the tree a natural orientation in the direction from root to leaves. The root represents the most recent common ancestor of all taxonomic units represented by the tree. Each internode represents the closest ancestor to its descendants. Usually these inner nodes represent hypothetical taxonomic units that currently cannot be observed. By contrast, the leaves of the tree represent real taxonomic units.

From a rooted tree it is possible to construct an unrooted tree at any time simply by removing the root marking, the reverse procedure is only possible with additional information about the evolution.

Phylogenetic tree of life

Comparison of taxonomic units

Phylogenetic tree construction is based on data on similarity between taxonomic units. There are many possibilities to define this similarity. More recently, knowledge in the field of molecular biology has been widely used. We rely on base sequences in the genomes of individual biological species, or information on relevant amino acid and protein products can also be used. Based on this data, it is possible to determine the genetic distances between each pair of taxonomic units. A precise calculation of this distance requires an appropriate alignment of the compared DNA sequences first. This is a computationally very difficult task (it falls within the class of NP-complete problems), so in practice a variety of heuristic methods are used that are able to find at least suboptimal solutions in an acceptable time. For aligned sequences, it is possible to determine the distance based, for example, on the percentage of different bases between sequences. More sophisticated methods attempt to estimate the number of mutations required to transition from one sequence to another.

Beyond the molecular biological data, the morphological properties of the taxonomic units studied may also be taken into account. The calculation of the distances in this case depends on the characteristics observed and the importance assigned to each character.

Phylogenetic tree construction methods

Distance-matrix methods

These methods are based on a distance matrix that indicates the distance spacing between all pairs of taxonomic units for which we construct a phylogenetic tree. Genetic distance is used as a distance in this case.

UPGMA (Unweighted Pair Group Method with Arithmetic mean)

UPGMA, simplified Clumping Analysis, is the simplest algorithmic method to construct a phylogenetic tree. The procedure is as follows:

1. Find the smallest value in the distance matrix (equivalent to the pair of taxonomic units closest to each other).
2. Combine the relevant taxonomic units into one group and calculate the distance of this new group to all other taxonomic units. The distance of the taxonomic unit T to this new group S is calculated as the arithmetic mean of the distances between the unit T and all the elements of group S. Furthermore, Group S can be considered as a hypothetical taxonomic unit.
3. If we have more than one taxonomic unit available, repeat the procedure from step 1.

By graphically representing the clustering process over the course of the algorithm described, we obtain the desired phylogenetic tree. The hypothetical taxonomic unit that was created last is its root.

Least Squares Method

In this case, we construct all sorts of phylogenetic trees and evaluate which one is the best. We can make the assessment according to the following prescription:

$\ Q=\sum _{i=1}^{N}\sum _{j=1}^{N}(D_{i,j}-d_{i,j})^{2}$,

where d_i,j is the distance between the i and j nodes in the rated phylogenetic tree and D_i,j is the distance between the corresponding taxonomic units in the distance matrix.

This procedure requires the design and evaluation of all possible phylogenetic trees, which, like aligning, is a NP-complete problem.

Minimal Evolution Method

The procedure is the same as for the least squares method, but we compare the individual trees by the sum of the lengths of all the branches.

Neighbor-joining

At the beginning, one star tree is created, where there is one internode, and all the solved taxonomic units are represented by leaves. This tree is gradually broken down by clustering the nearest taxonomic units so that the total length of the tree is reduced as much as possible in each step.

Maximum parsimony

The method of maximum parsimony seeks to find such a phylogenetic tree, which requires as few evolutionary events as possible, which would have to occur if this tree matched the course of evolution. In some cases, different weights are assigned to individual evolutionary events when assessing trees, such as when certain nucleotides or amino acids are known to mutate more easily or worse than others.

In the basic variant, this method again requires the design of all possible phylogenetic trees and their subsequent evaluation. Branch and bound method, for example, can be used to streamline searches through trees by selecting only "hopeful" trees.

Method of Maximum Likelihood

Here it is based on statistical methods and posterior probability. We are trying to estimate what the probability is that the statistical hypothesis presented by a particular phylogenetic tree is valid for the data we have available. For the H hypothesis and the D data, this probability can be calculated as follows:

$\ P(H|D)=P(H).{\frac {P(D|H)}{P(D)}}$,

where P(D|H) is the probability that we observe actual D data, assuming the H hypothesis is true.

The method requires a substitution model, on the basis of which we determine the probability of individual evolutionary changes (mutations). A tree that needs more of these changes to explain available phylogenetic data will have less credibility than a tree that makes do with fewer changes. Beyond that, we also notice the lengths of the individual branches.

Links

Related articles

• Phylogenetic taxonomy
• Evolution

External links

• Phylogenetic tree on Wikipedia

Sources

• Vladimír Hampl: Přednáška z molekulární taxonomie
• Computational phylogenetics on Wikipedia