Electrochemistry

Electrode events

[ ✎ edit embedded article ]

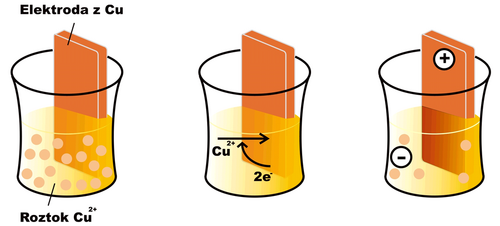
If we dip an electrode made of the same metal (in this case copper) into a solution of a metal ion (e.g. Cu²⁺) an oxidation-reduction reaction begins to take place on the surface of the electrode

Cu²⁺ + 2 e⁻ < = > Cu

In the case of copper, under normal conditions, the equilibrium of the mentioned reaction is shifted somewhat to the right (for other substances, e.g. zinc, the opposite can be the case). A layer of reduced copper is deposited on the surface of the electrode, and the electrode gradually acquires a positive charge, as free electrons are drawn from it. The solution in which the electrode is immersed, on the other hand, acquires a negative charge, as Cu²⁺ cations are depleted from it without replacement . After a certain time, the reaction stops, as electrostatic forces prevent the further movement of charged particles, and an equilibrium characterized by a certain electric potential at the electrode is established. The effort of the electrode to receive or give up electrons is characterized by the so-called reduction potential (E_red). If all components of the electrode reaction have an activity equal to one, or are in a form to which the standard state is related (e.g. solid state), we speak of a standard reduction potential (E⁰_red).

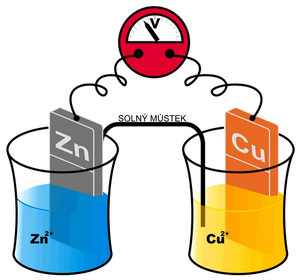
We cannot measure the potential created in the manner described above on one electrode directly. However, we can create a cell composed of two different electrodes – eg metals (generally semi-cells) and two corresponding electrolytes. An example can be the so-called Daniell cell: Cu in a solution of Cu 2+ and Zn in a solution of Zn 2+ . Depending on whether individual metals tend to be more oxidized or reduced, we can arrange them in the so-called Beketov electrochemical series (K, Ca, Al, Zn, Fe, Ni, Pb, H, Bi, Cu, Hg, Ag, Au). For these purposes, the electrode potential of the so-called standard hydrogen electrode is considered ero. Metals that have a negative standard reduction potential and therefore readily donate an electron are in the row to the left of hydrogen (ie. potassium tends to oxidize to K⁺). Metal ions that are on the right, on the other hand, accept electrons easily (eg. Ag⁺ is easily reduced to Ag)and their standard reduction potential is positive.

Daniell's article mentioned above is schematically written Zn | Zn²⁺ || Cu²⁺ | Cu (the more negative metal is written to the left). A redox reaction takes place at the zinc electrode

Zn²⁺ + 2 e⁻ < = > Zn,

which has an equilibrium constant K_Zn and is characterized by a standard reduction potential E⁰_red(Zn);the above reaction takes place on the copper electrode

Cu²⁺ + 2 e⁻ < = > Cu

with the equilibrium K_Cu and the standard reduction potential E⁰_red(Cu). In the given case, K_Cu > K_Zn, or E⁰_red(Cu) > E⁰_red(Zn). In other words, copper will be reduced and deposited on the electrode more readily than zinc. Thus, more electrons are consumed from a copper electrode than from a zinc one. Ultimately, the copper electrode will have a positive voltage to the zinc that we can measure.

If we let a current flow between the electrodes, the „convergig" electrons will be supplied to the copper electrode from the zinc electrode, and the resulting process can be written as follows:

Zn → Zn²⁺ + 2e⁻

Cu²⁺ + 2e⁻ → Cu

Current will flow through the conductor between the electrodes and the salt bridge until the zinc electrode dissolves, or (which is more likely) until Cu²⁺ from the electrolyte is consumed, or the second electrolyte becomes saturated with Zn²⁺ ions (discharge of the electrochemical cell).

The cell voltage is equal to the potential difference of the two electrodes. A cell on which events take place spontaneously („produces“ voltage) is called a galvanic cell (ΔG < 0). If we apply a voltage to it and the events are "forced" by the applied voltage (ΔG > 0), we call such a cell electrolytic.

The electrode processes described are relatively general and take place in a similar way in various systems composed of various metals and ions.

 For more information see electrochemical potential.

.

pH-metric

[ ✎ edit embedded article ]

</noinclude> The oldest and still most widespread ion-selective electrode that is used to measure pHis the glass electrode. As a rule, it is constructed in one body directly with a suitable reference electrode. There are a number of modifications; here we will show the principle on the basic design.

Glass electrode

The ability of the glass electrode to indicate the concentration of H⁺ can be simply explained by the fact that the glass membrane (a well with very thin walls blown from special glass) is permeable to H⁺ and impermeable to other ions. A silver wire covered with a layer of AgCl is immersed in the internal electrolyte. Depending on the acidity of the measured solution, the concentration of H⁺ inside the flask changes. Cl⁻ ions do not pass through the membrane, so in order to maintain the electroneutrality of the solution, the reaction takes place at the electrode

AgCl + e⁻ < = > Ag⁺ + Cl⁻.

If we immerse the electrode in an acidic solution, the excess of H⁺ ions will cause more Cl⁻ ions to be released from the AgCl paste. This consumes more electrons from the silver wire and the electrode gets a more positive voltage compared to the reference. Conversely, in an alkaline environment, excess Cl⁻ will donate its electrons and the electrode will have a more negative voltage.

A silver wire coated with AgCl paste is most often used as a reference electrode in pH-metric, but this time it is immersed in a KCl solution with a precise concentration (i.e. in a solution with a constant concentration of Cl⁻, e.g. saturated, 1 mol·l⁻¹, 3 mol·l⁻¹ etc.). The potential of the reference electrode is not affected by the concentration of H⁺ ions. The electrolyte of the reference electrode is conductively connected to the measured solution by means of a bridge with a ceramic partition (frit).

The given description of the pH-metric electrode is greatly simplified. The actual steps on the glass membrane are described in the glass electrode details subpage

Electrolysis

[ ✎ edit embedded article ]

In the interpretation of electrode events , we assumed that the system is in an equilibrium state. Let us now consider what happens if we apply voltage to the electrodes from an external source (electrolytic cell, ΔG > 0). The ongoing events will be governed by Faraday's laws . In order for electrolytic reactions to take place, the voltage on the electrodes must exceed a certain value - the breakdown voltage (corresponds to the sum of the standard electrode potentials for individual reactions).

As an example, we will use a system consisting of two inert (platinum) electrodes in an aqueous solution of sodium chloride.

General scheme of electrolysis.

If we apply a voltage to the electrodes, the ions in the solution begin to travel according to their charge, Na⁺ and H⁺ cations to the cathode and Cl⁻ and OH⁻ anions to the anode. Reactions will take place at the cathode (and in its immediate vicinity):

2 H⁺ + 2 e⁻ → H₂ ↑

and (at higher voltage):

Na⁺ + e⁻ → Na

2 Na + 2 H₂O → 2 Na⁺ + 2 OH⁻ + H₂ ↑

A reaction will take place at anode:

2 OH⁻ → H₂O + ½ O₂ ↑ + 2 e⁻

and (at higher voltage):

2 Cl⁻ → Cl₂ + 2 e⁻

Chlorine will be partly released as a gas, partly it will further react with water to form hydrochloric acid and hypochlorous acid:

Cl₂ + H₂O → H⁺ + Cl⁻ + HClO

The resulting gases will escape from the system (in this case, it is therefore an irreversible event). We also know the above example from practice - notice, for example, the bubbles at the electrodes during electrophoresis.

Use

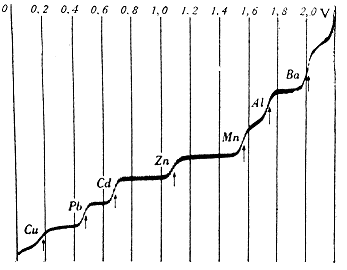
Polarographic curve, dependence of current on voltage. Taken from

This phenomenon is also used, for example, in polarography. Simply put, if we gradually increase the voltage across the electrodes, only a small current will initially flow through the system. After reaching the breakdown voltage, characteristic of the respective redox couple, electrolytic processes begin to take place on the surface of the measuring electrode and the current increases sharply (the rising part of the polarographic curve). Since this reaction is very fast, the ions around the electrode will soon be depleted. New ions reach the surface of the electrode by diffusion, the speed of which is limited, so that the intensity of the current does not change much (flat plateau). If we construct a graph of the dependence of the current on the input voltage, we get a step-like polarographic curve.