Limit of microscope resolution

From WikiLectures

Thanks to the microscope, we can improve the resolution of the eye by up to two orders of magnitude, i.e. 0.001 mm. The task of the microscope is to distinguish individual objects, or details, and enlarge their image so that it corresponds to the size parameters of the eye, i.e. the objective creates an image and the task of the eyepiece is to increase the angle of observation to a size suitable for the eye.

The resolution of the human eye
  • the point resolution limit of the eye is approximately 1'
  • the smallest object size that the eye can distinguish is 0.1 – 0.15 mm

In the case of a tired eye, the values ​​are different.

The most appropriate measure of the resolving power of a microscope, or rather its objective, is the resolution limit.

Limit of microscope resolution[edit | edit source]

It is the distance between two points of the object when we can still distinguish them, i.e. they do not merge into one point.

The resolution limit of the microscope affects

Bending and interference of light[edit | edit source]

Bending and interference will be explained on the preparation, which we will consider as a planar optical grating. As light passes through the grating, light interference occurs and maxima and minima occur. The rays strike the grid parallel and their direction is perpendicular to the plane of the grid. If the grating constant is small enough, interference of light waves and partial bending of their direction will occur when the beam passes through the slit. The maximum luminous flux passes through the grid mainly in the original direction, but due to the wave properties of light, it is partially weakened. In a plane perpendicular to the direction of the beam, light is distributed into alternating maxima and minima. The intensity of the maxima decreases rapidly with increasing distance from the original beam, and thus we distinguish maxima and minima of several tenths of order depending on the distance from the original beam. Due to the bending and interference of light, the image of a point in a real optical system will not be a point, but a scattering surface, or a scattering (bending) ring.

Abbe's resolution criterion: For the formation of a resolved secondary (real) image of the optical grating, the primary image must contain not only the maximum of the zeroth order, but also at least the maximum of the first order. The image is created by the superposition of bundles of different bending maxima - i.e. the higher the quality of the image, the greater the number of bending maxima involved in its creation. If two objects are so close together that their scatter rings partially overlap, they will not be distinguished and will be displayed as one.

Based on Abbe's criterion, we can form a relation for the resolution limit of the microscope:

It applies: d = λ / A
λ…..the wavelength of the light used
A….numerical aperture

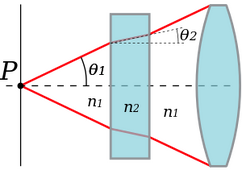
The numerical aperture relative to point P depends on half the apex angle θ of the maximum light cone that can enter or exit something.

Numerical aperture[edit | edit source]

In the literature, it is abbreviated N.A. or n.a. It is a dimensionless number that is a numerical measure for the ability of microscopic optics to capture information contained in the observed object. It is true that the lens with a higher numerical aperture (at the same magnification) has better quality. Numerical aperture is therefore the most important aspect for comparing the quality of objectives, and manufacturers aim for a microscope with the largest possible numerical aperture.

It applies: A = n. sin α
n…. index of refraction of the environment (between objective and specimen)
α….the angle between the central and peripheral rays of light entering the lens

Condenser construction diagram

Condenser[edit | edit source]

The condenser must be set in such a way as to concentrate the light flux as best as possible into the plane of the specimen and into the entrance pupil of the objective. This can be achieved by a suitable height adjustment of the condenser table and a suitable setting of its numerical aperture. The numerical aperture of the condenser can be controlled by an aperture stop. For the condenser, the resolution limit relation generally applies:

d = λ/(Aobj+Acon)

When the lens and condenser are optimally matched, their numerical apertures are the same. In practice we use Acond < Aobj

It follows from the relationship that the ability of the lens to distinguish two close object points in the light passing through the condenser and to display them as two points, not as one point, is not determined by the magnification of the lens, but by the numerical aperture and the wavelength of the light used.

The closer the two points can be distinguished, or the smaller the distance "d" between them, the better the resolution of the lens.

Lens defects[edit | edit source]

Links[edit | edit source]

Related articles[edit | edit source]

Sources[edit | edit source]

  • HEJTMÁNEK, Milan. Úvod do světelné mikroskopie. 3. přeprac. a dopl. vyd. Olomouc: Vydavatelství University Palackého, 1993, 65 s. ISBN 80-706-7308-7.
  • SMÉKAL, Petr. Experimentální metody biofyziky II. 1. vyd. Ostrava: Ostravská univerzita, 1995, 712 s. ISBN 80-704-2723-X.
  • PROSSER, Václav a kol. Experimentální metody biofyziky. 1. vyd. Praha: Academia, 1989, 712 s. ISBN 80-200-0059-3.

External links[edit | edit source]

Categories: Histology, Exam questions from biophysics (2. LF UK)/Light microscopy, Significantly changed checked articles

Retrieved from "https://www.wikilectures.eu/index.php?title=Limit_of_microscope_resolution&oldid=56814"